zwischendurch ne kleine matheaufgabe. wolf und ich stellten uns dieser tage die frage, wann er doppelt so alt wie seine tochter war. wolf fing an, auszuprobieren, scheiterte aber. er 100, sie 50? das kann nicht sein. mein vater ging mit leichter hand an die lösung. und zwar berechnete er die differenz der beiden alter und schrieb:

Wenn ich die Differenz mit 2 multipliziere, habe ich das Alter, das ich haben muss, um doppelt so alt wie Du zu sein, also war ich mit 56 Jahren doppelt so alt wie Du.

elegant! als ich ihn fragte, wie er das begründen würde, fiel ihm nichts ein, es war eben ganz natürlich, so zu rechnen.

die mathematik geht von klar definierten vorgaben aus, und die gleichung, die zum ergebnis führt, enthält nichts als diese vorgaben.

es gibt zwei voraussetzungen, aus denen wir in unsere gleichung formen. zunächst mal: das alter von laura soll doppelt so groß sein wie das alter von peter. das kann man so hinschreiben:

petersAlter mal 2 = laurasAlter

damit ist die erste bedingung in die gleichung eingeflossen. würden wir jetzt peter, der jetzt zum beispiel 18 ist, einsetzen, und laura, die zum beispiel 25 ist, bekämen wir einen widerspruch:

18 mal 2 ist nicht 25, sondern 36

woran liegt das? es liegt daran, dass wir ja nicht peters alter heute suchen, sondern in soundsovielen jahren. in wie vielen jahren, wissen wir noch nicht.

petersAlterDann mal 2 = laurasAlterDann

sehen wir uns mal die zahl der unbekannten an: wir kennen das heutige alter der beiden, wir haben die zahl 2, mit der wir rechnen können. was suchen wir? wir suchen das Dann in petersAlterDann und in laurasAlterDann. das Dann ist die zahl der jahre, die wir zum aktuellen alter addieren müssen. nennen wir diese zahl t. das machen die mathematiker gern, wegen tempus = die zeit.

(peterAlter + t jahre) * 2 = laurasAlter + t jahre

da steckt übrigens unsere zweite voraussetzung drin. sie scheint trivial, und er lautet: peter altert im gleichen tempo wie laura! sein alter bleibt nicht stehen, sie altert nicht schneller, es geht schön synchron. deswegen können wir zu beiden altern dasselbe t addieren. man kann jetzt die tatsächlichen alter der beiden einsetzen und das t ausrechnen. das machen mathematiker nicht gern, sie formen die gleichung lieber um wie in der handschriftlichen darstellung oben. dabei kommt heraus:

t = laurasAlter – 2 * petersAlter

angenommen, wie im beispiel oben, peter ist heute 18, laura 25, dann ist

t = 25 – 2 * 18 = 25 – 36 = – 11

die frage war: wann war peter halb so alt wie laura? die antwort lautet: vor 11 jahren. die probe: peter war da 7, laura 14; passt. wird peter jemals wieder halb so alt sein wie laura? nein, denn unsere gleichung hat nur eine lösung. es gibt andere gleichungen, die auch mehrere lösungen haben können, diese hier aber nicht.

schließlich noch ein besuch bei dem englischen mathematiker stephen wolfram. so sieht er aus:

stephen wolfram. foto: stephen faust, wiki commons

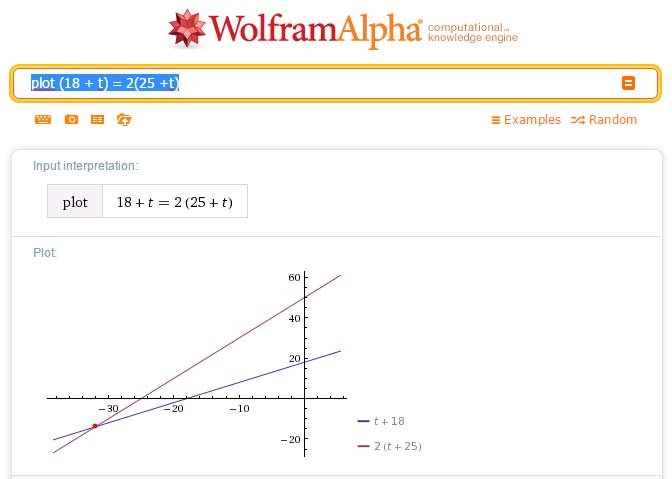
wolfram ist der berühmteste visualisierungsexperte unserer zeit. sein weitgehend kostenlos nutzbares portal (gibt es auch als app) ist regelrecht gierig, uns die grafische lösung für unsere gleichung zu zeigen. man macht das dort mit dem befehl “plot”. gehen wir also zu wolframalpha.com, geben dort ein:

plot (18 + t) = 2(25 +t)

dann erkennt die webseite, wir haben links die funktion für eine gerade und rechts eine funktion für eine gerade, und zeichnet uns zwei geraden ein. die blaue ist die von peter, die lilafarbene die von laura: